前言
暑假的時候申請上了數學系的輔系,所以這學期課表大致就以系上的必修+輔系的必修為主體了。
修課清單:
- 系訂必修
- 線性代數 Linear Algebra
- 演算法設計與分析 Algorithm Design and Analysis
- 自動機與形式語言 Formal Languages and Automata Theory
- 輔系必修
- 線性代數一 Linear Algebra(1)
- 分析導論一 Introduction to Mathematical Analysis(1)
這次我的選課策略沒有把課表塞的滿滿滿,一方面是我覺得這學期修的課和以往的風格差蠻多的,而且也沒有那種能靠抱大腿就一切安好的課,所以只要能把有修的課都顧好、甚至於有閒暇的話還能自己更深入的看課本以外的東西的話我就很滿足了。
除此之外我的選課還有幾個值得說明的地方。
我做了一個如果沒說,會讓人以為這人要從資工系跑路了的決定,那就是把二上必修的系統程式設計退掉,原因在於他和分導的時間衝堂了,因為我對分導的內容比較有興趣而且又想說好像sp明年再修完也不會怎麼樣,所以做了這個隨便的決定(現在想來我真的覺得我好勇)。
另外我的課表裡面有兩門線性代數,這是因為由於學校的規定(細節省略),如果要帶輔系畢業的話一定要兩邊的線代都修,雙主修才能只修數學系的。雖然畢業了以後輔系應該是沒什麼用,不過我預期多修一個系上的線代應該是不會增加多少負擔,說不定還能洗一點GPA學到一些「資工特化」的線代應用,所以就乾脆同時修兩邊了。
最後還有先跑去修大三必修的自動機與形式語言,我考慮的是這門課不太需要什麼基礎,而且如果先修了,那明年如果我想修數學系的常微分方程導論的話就不會撞課了。另外我也對這門課的內容很感興趣,完全沒有理由不提早修這門課,所以就簽了。
每一門課我都會列出四點數據:
- 甜度:學期成績好不好拿高分(非常主觀)
- 負擔:要花多少時間在這門課上(以該學分而言)以及會不會和其他課一起來壓你
- 收穫:修這門課學到多少東西或是有什麼比較難自己取得的機會
- 課後學習時數(每週)
另外還有如果讓我再選一次的話,我還會不會選擇這學期修這門課(or 別的學期也不會修)
系訂必修
線性代數
- 授課教授:呂學一
- 學分:3
- 等第:A+
- 一句話帶過:我只是來水學分的
- 甜度:🌟🌟🌟🌟🌟🌟🌟⚫⚫⚫
- 負擔:🌟🌟🌟⚫⚫⚫⚫⚫⚫⚫
- 收穫:🌟🌟⚫⚫⚫⚫⚫⚫⚫⚫(這是以我同時修數學系線代的觀點打的分,不代表別人來修也會沒收穫)
- 課後學習時數:2.5小時(平均)
- 會不會再修:會
原本負責雙班線代的是李明穗教授,但是好像因為他臨時有事所以初選前臨時改成呂學一負責雙班,以前呂學一就教過線代了,不過據他所說,今年他是完全重新編教材,也用了和以前不一樣的教法。
第一週就有講到大致是跟著Friedberg來教,同時也是數學系用的課本,和單班用的課本不一樣,只有第六章(內積空間)的部分因為他有自己的想法,所以教的「順序」是和課本不一樣的。我就想說我應該是只要去聽數學系那邊的,這邊都不用來上課應該也沒關係,所以我第二週就沒去上了。原本想這樣好爽喔都不用上課就有3學分,可惜事實並沒有我想像的那麼好,因為數學系的線代是全年課程,所以他們是把第六章規劃在下學期教,可是學一不等人,大概在第13週的時候就進到第六章了,所以我第14+15週有去課上聽。
這門課就跟所有呂學一的課一樣,都是
- 0作業
- 三次段考
- n題取最高分的(n-2)題
- 黑箱給等第
- 沒上課錄影
比較值得一提的可能是他課程介紹的時候有說考試是100%證明題,不過其實第三次段考他有考幾題計算題。另外雖然沒有作業,但是他會在cool上放一點練習題,真的只是一點點而已,難度可能大概是段考的普通題?可能因為對這種上課模式的恐懼,所以學期初系上和我比較熟的人大部分都跑去加簽單班了,聽說只要在那間教室待到最後,教授就全部都會給加簽,即使他剛開始會叫外系的人離開。
在修之前有聽過系上大學長講到,以前他教線代的時候會自己給定理取名字,比如什麼小菜定理、濃湯觀察之類的,作為他真的有重新備課的證明,今年的名字又重取了。原本我想說如果只是在課上為了講解方便才取名字應該是也還好,但是課餘時間聽著同學們都在說什麼直和定理、投影觀察三、怒空觀察之類的時候,還是會讓我懷疑以後到底還能不能跟系上同學討論線代。除此之外,第二次段考出現了「請敘述我們課堂上所介紹的有限維向量空間上面(『訂製』線性轉換)的『訂製觀察』」,所以如果有明年要修課的人看到這篇文的話,一定要記名字或是把名字寫在單面A4大抄上,不要重蹈我的覆轍。
我前兩次段考基本上都是考前臨時看他的簡報做一張大抄,把過程當複習而已,不過第三次段考比較特別的是因為我沒老本(?能吃,所以需要真的去細看他的簡報在寫什麼,看到後來因為我時間分配燒雞了,而且我猜我前兩次有考的足夠好到這樣做也夠A+,所以我就直接把第15週的內容放掉不看了,想說等到線代二再來好好的學。結果也確實和預期的一樣,三次期考總分263/300,被調到A+。
段考助教改的超級鬆,真的是謝謝他們。我三次段考拿到的分數都比剛考完的時候自己估的高個20分左右,尤其第二次段考我的考卷上被寫了一堆「Why?」,我一看內容就知道考試的時候我想要唬爛過去,但是助教還是都給全對,除了第一次段考我沒想到就算是在資工系也不能隨便除以2以外,都是有寫的都對。另外有一題我偷開了上課應該是沒有教的選擇公理,助教也是給我整題的分數,只能說很爽,或者助教可能也不知道上課到底什麼有教什麼沒教,因為我看別人在吵分的時候助教也會問他考卷上寫的「跨界觀察」是什麼。
在前言的部分我有提到,原本想說其中一個來修本系線代的誘因是或許能學到一點「資工特化」的線代,但是結果並沒有達到我想像中的效果,也可以說數學系線代講到的應用比本系還要來得多。另外可能因為時間安排問題,第六章的內容講的非常緊湊,甚至於蠻大一部份的內容他都是叫我們回家自己看,然後投影片按按按跳頁數,我不知道他是不是原本就打算這樣,不過學期初和學期末的講解細緻度差別蠻大的。如果教授一開始的目標就是放在只要把Friedberg飆完,其他都是次要的話,好像就說得通為什麼會有這兩點了。
不對啊,如果他只是想把Friedberg飆完的話為什麼第一週要花三節課來講Group和Field,我還是不理解。
這門課有關成績的部分蠻不透明的,等第是黑箱給的,考試也不公布平均,說是希望學生們不要比較彼此的成績,修了就盡量撐到底。因為我只有學期初和學期末有去上課,如果只看教室有多少人來判斷的話,停修的人可能蠻多的?我不知道不公布平均對鼓勵不停修有沒有幫助。也因為黑箱給等第,所以我甜度的七顆星星其實是亂打的。
演算法設計與分析
- 授課教授:呂學一
- 學分:3
- 等第:A-
- 一句話帶過:
- 甜度:🌟🌟🌟🌟🌟⚫ ⚫⚫⚫⚫
- 負擔:🌟🌟🌟🌟⚫⚫⚫⚫⚫⚫
- 收穫:🌟🌟🌟🌟⚫⚫⚫⚫⚫⚫
- 課後學習時數:4小時(平均)
- 會不會再修:會去抽抽看換班
去年原本是陳縕儂+蕭旭君合班上課,不過不知道是不是因為一些所有人都懂的原因,今年改成拆班,單班是蕭旭君而雙班是呂學一,我因為那個時候覺得想跳班的動機沒有特別強烈,而且看一堆人搶破頭想抽籤跳去單班,也有人是如果沒抽到就寧願明年再修的,所以就沒有去佔原本就很缺的加簽名額了。
跟線代一樣,剛開學的時候完全沒有課程大綱,我因為好奇跟隔壁班內容的差異所以第一週上課的時候有私底下有去問教授,不過他自己課都還沒備完所以他也不知道會教什麼東西。
這門課就跟所有呂學一的課一樣,都是
- 0作業
- 三次段考
- n題取最高分的(n-2)題
- 黑箱給等第
- 沒上課錄影
蕭班的內容看起來應該是沿襲以前合班時的教學規劃,原本我想在學期期間的時候就交互看兩班的內容來彌補兩班內容上的差距,不過後來呂學一用第一週講了數學之美、把均攤拉到前面,然後用兩週飆完分治、DP和Greedy。發現兩班教授的想法的差異有多大以後漸漸地就沒繼續做了。另外他還有把蕭班當作分治的其中一個例子的平面最近點對的演算法拉到後面才講,好像是因為原本教授把計算幾何當成一個獨立的主題所以才這樣安排,但是後來因為時間關係所以來不及講其他計算幾何的演算法了,明年他說不定會講多一點計算幾何。
事後比較兩班的上課內容的話應該可以說差蠻多的,因為我的國文寫作能力很爛所以用條列的好了,希望沒有列錯的,沒有特別註明的項目是呂學一比起隔壁班多講的東西:
- $\lim_{n\to\infty}\frac{f(n)}{g(n)} = c > 0 \implies f(n) = \Theta(g(n))$等等的極限相關公式全部不能用,因為和隔壁班不一樣,在這裡的函數的值域是整個實數,雖然我不知道為什麼代表某個演算法操作的函數可以有負的,不過反正實際寫這個公式的證明的時候會發現可不可以是負的有差
- 會教我們在演算法研究的世界裡會出現$O(n)^{O(logn)}$或者$O(O(g(n)))=O(h(n))$這類東西,不過我沒聽漏的話整個學期都沒出現相關例子
- 如何計算一個演算法的「下界」,並不是像算上界一樣把每一行用的時間加起來
- 這一班會教不只探討演算法的時間複雜度上下界,還有提到一個「問題」本身也有上下界以及他和演算法上下界之間的關係。
- 我懶得對簡報了,反正圖論多了一點東西,比較大的差異可能在講Prim’s Algorithm的時候有講到Fibonacci Heap(呂學一覺得是這門課裡最複雜的東西),還有多了Maximum flow
- P/NP的部分我也懶得仔細比較了,反正看起來兩邊都多講東西到彼此沒講到的東西。比較有趣的是兩班對於NP的定義是不一樣的,蕭班是可在多項式時間內驗證,呂班是存在non-deterministic的多項式時間演算法,不過自動機會證明這兩個定義是等價的,非常推薦有能力的話大二就修自動機
- 蕭班有Linear Programming我們沒有
- 兩班講隨機演算法的例子不太一樣,呂學一有順便帶出通訊複雜度的概念
大概這樣吧,有漏東西就漏吧隨便了
考試的話好像大概會有6~70分是抄上課的證明,我沒特別算不過大概是這樣,啊我的分數也差不多就70多。第二次考試考了特別多上課演算法證明,抄完證明以後我根本沒多少時間想創意題,上大學以來第一次有了可能會被當的感覺。
回憶起來我DSA的時候期考就考很爛,大概只有比平均好一點點而已,不過那個時候至少DSA有作業,而考試也考的是類似概念的題目,所以我還不會在考試的時候被題目單方面揍還不了手,畢竟作業有練習過嘛。但是呂學一ADA完全沒有作業,所以我覺得我準備的超級不充分,或者說我根本不知道怎麼準備,能做的只有去理解上課證明。
大一的時候有在VVN把上課影片全部下架前看了一下(不過沒有看蕭旭君的部分),相比之下我還是比較喜歡呂學一的上課方式,因為他自己的研究領域就是演算法,所以他的講法常常會伴隨很多演算法領域的研究歷史,讓我們知道一大票發明上課講到的演算法的人之後都拿了圖靈獎,另外還有一些可能和演算法研究比較相關的東西,而不是把課本上的證明全部照唸一遍。
但是即便如此,我在這門課的學習效果還是非常差,我覺得問題在於沒有作業。雖然好像很多人覺得很煩,但是我還蠻喜歡DSA的手寫作業的,我覺得對我的學習真的有很大的幫助。但是呂班完全沒有作業,所以我感覺我會的只有背上課怎麼證演算法的,感覺非常不踏實,也不覺得有學到很多(和預期相比),然後考試還考超爛,或許這個班級還是比較適合原本就都會的人來聽故事?反正我考試考這麼爛應該代表我不適合這個班。
甜度五顆星跟線代一樣是亂打的,一樣是黑箱調分。
自動機與形式語言
- 授課教授:林智仁
- 學分:3
- 等第:A+
- 一句話帶過:其實是計算理論
- 甜度:🌟🌟🌟🌟🌟🌟🌟🌟⚫⚫
- 負擔:🌟🌟⚫⚫⚫⚫⚫⚫⚫⚫
- 收穫:🌟🌟🌟🌟🌟⚫⚫⚫⚫⚫
- 課後學習時數:1.5小時
- 會不會再修:會
因為Tony(陳偉松)跳槽去利物浦大學了,所以另外一班變成林忠緯帶。剛開學的時候兩班我都有簽上,我依稀記得在哪裡有看過以前學長姐好像有人會因為林智仁歷年A+都只給10%所以跑路去隔壁班,不過我發現同屆的一堆強者都在林忠緯班,感覺在林忠緯班會被大炸魚,而且林忠緯開學的時候好像有講兩班切比例的方式會一樣,因此忠緯班的成績誘因對我來說其實沒很高。
會讓我選這班比較關鍵的原因是我覺得兩個教授相比,我之後比較有可能再修林智仁的課而不是林忠緯的課,所以來修這一班可以稍微熟悉一下他的上課模式(結果下學期好像林智仁的兩門課都沒了QQ,不知道是不是以後都不開課了)。另外林忠緯班的作業是不計分的,我自認比較不會考試,所以這也是我選擇這班的主要原因之一。
這門課的一開始教授就特別說他覺得這門課與其叫自動機與形式語言,應該叫做計算理論,因為這門課就是在講計算理論,確實,我覺得把課名叫自動機與形式語言直接用兩個專有名詞夾擊別人不太好,至少我大一的時候第一眼看到這門課的名字會覺得完全不知所云。
這門課的進行方式是教授會在上課的時候播學期一開始就全部預錄好,完全公開在另外架的課程網頁上的影片,這個我是聽別人說的,因為我直到學期結束都從來沒到場上過課。原本第一週我有想去聽的,但是我在捷運上突然大爆暈,在東門站撐不下去了直接下車,幾乎失去意識地倒在一根柱子旁邊,來關心我的站務人員人超好的,不過我好像聽到他跟同事說我是大安高工的學生。
因為我想為我從來沒出席過找理由所以岔題了,基本上整學期我都是照著自己的步調看影片,教授在影片裡都是用英文講,而且語速超級慢以至於我都開1.75倍速看,之前在Office Hour的時候跟他實驗室裡的助教聊到,他們說這是教授故意的,他平常講話沒那麼慢。
作業的部分基本上就是超級基本題+以前的期考考古,而且以前的考古詳解都是公佈在以前的課程網頁上的,所以只要邏輯清楚而且沒有粗心的話,作業滿分我想應該是很好拿的?邏輯清楚的部分,我也是真的修了這門課以後才明白為什麼陳偉松會想在上個學期開基礎數學寫作了,要說這門課的先修的話一定就是他了,可惜來年應該是再也看不到那門課了。
雖然說以前的考古有詳解,但是有的詳解是錯的,連帶的讓我第二次期考被扣了一個小分,去問助教了以後助教的回應是那就是錯的,不過他們還是會把它擺在上面陰人之類的,有之後要修的同學看到這篇心得的話就算你們賺到了,以前期考有一題要求畫Turing Machine的題目,詳解把Accept State畫了兩個圈圈,但是那是不對的,Turing Machine的Accept State不可以有兩個圈圈。
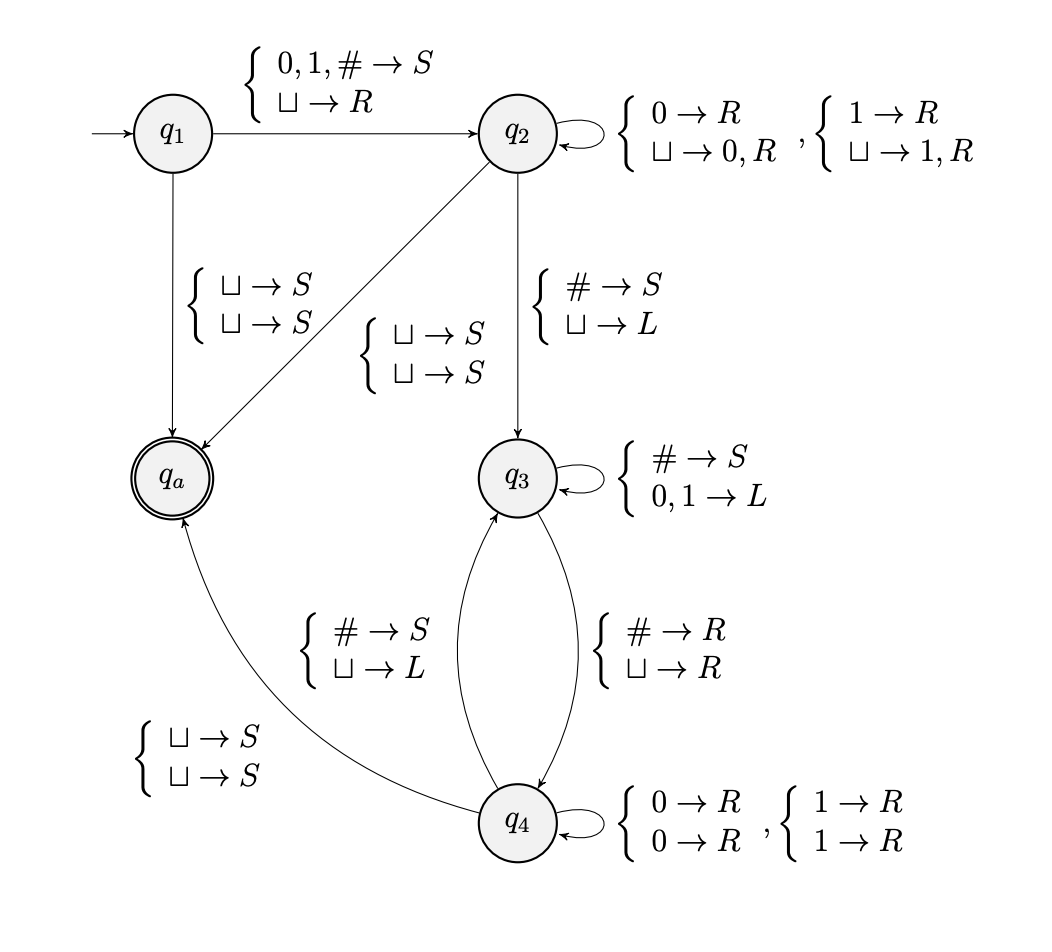 |
|---|
| 解答的$q_a$有兩個圈圈 |
另外我覺得值得一提的是我覺得這門課的期考題目出的難度恰到好處,不會有很偏門的東西,而且瘋狂刷題其實也不會佔到多少便宜,基本上只要觀念通,懂定義在幹嘛,剩下的就是看能不能通靈到題目想讓你通靈的東西了,寫起來有點像智商測驗。最有意思的是,他的題目超級無敵「素養」的,第一次和第三次期考他都在題目裡混進了跟自己研究領域有關的東西,另外課程網頁上用遮部分學好來公布全班成績的方式也被他出進了題目,寫起來真的特別有意思,也不用想靠猜題來對付他的期考了。也因此,讀這門課花的時間其實不算多,講誇張點,吸收能力強的話可能看完他錄的影片以後就能來考試了,砸時間下去讀的邊際效益蠻低的(這是對於如果只在乎成績的人來說,這門課還是有超多好玩的東西能自己讀的)。
要說缺點的話,我覺得教授錄的影片基本上就是課本節錄版,前2/3學期我基本上都自己看課本,反正講的東西都差不多。另外感覺這門課超級慢熱的,前2/3學期都在讓我們熟悉計算模型的概念,直到後1/3學期才出現了這門課的重點(應該吧,我覺得後面才是重點),比如Decidability、從Turing Machine視角出發的Time Complexity…等等。
課上我也學到了一些能用在系上其他課上的東西,比如學期末ADA和自動機都在講P/NP的時候,由於這門課經常用到"undeterministic"的概念,所以比較好理解呂學一上課講的「隨性演算法」到底是在隨什麼。除此之外,NASA一階的時候作業有遇到一個有關ReDos的題目,那個時候我因為看不懂原理所以只有照著生會讓不好的扣TLE的輸入資料,不過聽完這門課前1/3講到的DFA、NFA與Regular Language之間的關係以後,我現在更能理解wikipedia上描述電腦處理Regular Expression的演算法,也更能理解為什麼當時能用那個測資搞題目寫的程式了。
修了這門課真的讓我感到很興奮,如同課程網頁上講的
Theoretical CS has some fancy/big ideas
我們能利用這種「簡單」的模型來解釋電腦究竟能做什麼、他又能做到什麼程度,這感覺就是很有美感的一件事。這給我的感覺就像是在小學我們看著三次方程式的根式解,想著到底誰能背起來這種鬼東西的時候,老師跟我們說四次方程式根式解是存在的,但是五次方程式的不存在,要證明這件事情我們需要定義什麼是Group…然後開始講一些讓人根本沒辦法直接想像這些東西到底跟算數有什麼關係的事情;而在這門課,我們開始考慮到底什麼是計算機能保證做得出來的問題,而為了解決這個問題,我們需要學習「如何在一條無限長的紙帶上面寫字」。因為我沒修過代數所以我不知道這個舉例恰不恰當,不過讓人想不到怎麼下手的問題能夠用抽象的新理論解決,這件事還是特別吸引我。
最後感覺能來比較一下兩班(畢竟另外一班第一次開),首先他們等第還真的用同一個比例切,所以林智仁班告別10% A+晉升成全班一半A字頭的大甜課了。
| 等第 | 等第比例 | 累積比例(由上而下) |
|---|---|---|
| A+ | 22.8% | 22.8% |
| A | 22.8% | 45.6% |
| A- | 5.3% | 50.9% |
| B+ | 14.0% | 64.9% |
| B | 16.6% | 81.5% |
| B- | 3.5% | 85% |
| C+ | 3.5% | 88.5% |
| C | 4.4% | 92.9% |
| C- | 5.3% | 98.2% |
| F or X | 1.8% | 100% |
除此之外,我不知道是不是因為語速的關係,隔壁班教的比我們班多一點點,而且我們其實沒講話課程網頁上的所有影片,比如Chapter5的Computation histories我們就沒講到。另外考試的差別也蠻大的,我們是考好考滿三節課,隔壁班則是一次考100分鐘左右,甚至還考一大堆是非題,不過我不確定他們其他題目有沒有比較難就是了。
輔系必修
線性代數一
- 授課教授:林惠雯
- 學分:4
- 等第:A-
- 一句話帶過:不只是線性代數的線性代數
- 甜度:🌟🌟🌟🌟⚫⚫⚫⚫⚫⚫
- 負擔:🌟🌟🌟🌟🌟🌟⚫⚫⚫⚫
- 收穫:🌟🌟🌟🌟🌟🌟🌟🌟⚫⚫
- 課後學習時數:7小時
- 會不會再修:一定會
這門課是我唯一一門到開學第一週還沒弄到課表上的課,因為初選人多到就算有輔系特權也沒辦法有填必上(說不定是數學系唯一一門這樣的必修),所以我就不管課表上蔡國榮開的線代導來教室加簽了,一下課想加簽的人就多到隊伍繞了教室半圈,每個想加簽的人教授都會先勸退個幾句:「你確定真的要修嗎?」、「不要啦,真的不要修啦」、「為什麼要這樣對自己呢」,我前一個人好像說漏嘴說自己有選上線代導,所以教授直接不讓他簽,最後是吵著吵著教授讓他先到旁邊等,不過因為我有先寄信給教授所以他直接給我簽了(好耶)。
林惠雯教授的課超級充實,他很喜歡和同學有互動,而且常常有一些我也不知道怎麼描述的「特色」,所以其實上課不會到太枯燥,上課時間抓得非常精準,每次上課都會把分配的進度講完,幾乎不拖課。
至於上課的內容也不會只有課本上寫的,比如他會用Zorn’s Lemma(並證明和選擇公理等價)來解釋為什麼任何向量空間都有Basis、用Permutation Group來解釋行列式交換兩行的操作為什麼是Well-defined的、用向量空間來解釋為什麼finite field的大小是某個質數的n次方、把T-invariant和module連結起來…可能因為教授的研究專業跟代數有關,他常常會把線代和代數會講的東西連結在一起,也可能他想給明年的代數鋪路。我第一次遇到一門完全不會想翹的課,唯一一次因為睡死所以翹掉的那天她用大一新生也聽得懂的方式來證明了代數基本定理。
據教授所說,今年她跟系上爭取到了大一必修課的考卷分ABC三種考卷的模式,
- A卷總分破百
- B卷是最普通的卷子
- C卷滿分70,不過都是基礎題
教授說A卷是給想拿A+的同學挑戰的(要A+一定要所有考試都考A卷),題目理所當然比較難,比如第一次小考和期中考就是給助教放飛自我,我自己是第一次小考考A卷,爆炸完回家看了助教寫的解答,不看不知道,一看就知道自己不可能在考試時間內想到這種作法,所以我就改成寫B卷了,B卷基本上就是上課證明+作業題型,不過我期末考計算題算太久+上課證明寫到卡住所以把我的等第炸掉了QQ。
這門課的作業是從課本裡勾題目,有上課的一天就有一份,加起來整學期有22份作業,課本題難度都還可以,不過學期後半段有助教出的Bonus題,會出現這種Bonus題有可能是因為第二次小考和期末考都改成全部教授出題了,助教的出題欲需要地方宣洩之類的。
另外今年有超愛玩的助教,學期初看起來還好好的,但是之後常常公告配梗圖發,還第一次讓我知道NTUCOOL上的課程列表是能換圖的。
 |
|---|
| 助教做的高斯消去髮,本人說他花了半小時做這張圖 |
我覺得這門課比起只是一門「超讚的線性代數課」,它更多的是「開給數學系學生的線性代數」,這門課的課程安排讓人看到線性代數不只是線性代數,他不是一門獨立的學科,他之所以是數學系大一必修就是因為他是各個學科的基礎,課內的內容有用線性變換的視角說明我們在微甲裡解線性齊次微分方程式的方法到底在幹嘛、用對角化來漂亮地解一種特定形式的多變數微分方程組、在Markov Chain的章節又和機率相關內容牽扯在一起。
在Markov Chain的章節實際上用到了幾個有分析風格的證明技巧,此時教授說了讓我印象深刻的話:
只會線性代數 做不了事 只會分析 可以做點事 但做不了大事 如果兩個都不會 就別幹這行了
這門課除了線性代數以外還帶給我了一點衝擊,聽起來可能很蠢,不過我是第一次遇到一門課是能和這麼多其他學科有關聯的,給我了一種開闊了視野的感覺。相較之下,呂學一的線代反而出乎我意料地相對沒怎麼講應用,有點把學期目標完全放在把Friedberg飆完,其他什麼都不管的感覺,感覺有點可惜。
分析導論一
- 授課教授:陳俊全
- 學分:5
- 等第:A-
- 一句話帶過:高等微積分
- 甜度:🌟🌟🌟🌟🌟⚫⚫⚫⚫⚫
- 負擔:🌟🌟🌟🌟🌟🌟🌟⚫⚫⚫
- 收穫:🌟🌟🌟🌟🌟🌟⚫⚫⚫⚫
- 課後學習時數:10小時
- 會不會再修:不會
還記得學期初系上同學知道我這學期修了這門課以後,常常第一句話是問我「分析導論在教什麼?」,我也是被問了以後才發現我不知道怎麼簡短地解釋,被問了幾次以後發現「高等微積分」好像是最方便的回答了,畢竟是舊的課名,所以好像蠻適合用來解釋的吧!但是說起來有點可悲,那就是這學期教授根本就講不到微分,更不用說積分了。
陳俊全教授的分導和其他教授有一個很大的不同,那就是他會花快半學期的時間來構造實數,這聽起來很扯,不過他真的到期中考為止只教了課本的第一章,他原本第一堂課上說的是目標兩個學期教九章的,應該可以宣告失敗了。
單純花時間在建構實數還不至於弄到半學期都卡在這裡,前半學期的上課進度非常緩慢,其中一個原因就是他的課上夾雜了非常多、超級多的語錄,一講講二十分鐘都不誇張,通常都是完全的題外話(不然就是關聯性超級牽強),而且常常同一個定理講好幾遍。相對的,教授在實數建構這一塊確實講的蠻鉅細靡遺的,但是進度已經拖到連助教都會私底下念的程度了。
不過後半學期好蠻多了,而且加上教授有事出國讓助教代了幾節課,助教上課的速度大概是教授後半學期速度的兩倍,所以最後講到了大約第五章一半的位置,不然教授自己的目標是能講完第四章就滿意了。
另外教授講話聲音偏小(至少和林惠雯比),學期剛開始坐在後面常常聽不到部分內容,所以我後來都盡量坐去前兩排了。
這門課的作業大約都一週一份,每份要花的時間差蠻多的,有那種花三個小時就能寫完的,也有看了兩三天以後才寫完的。總體而言,感覺起來完全沒有像其他教授的課程評價那樣的硬,至少不會大部分的時間都投注在這門課上,而且如果只是想拿分數的話可能也不用全寫,助教根本就改不完作業所以後半學期都跳著改,我有一個認識的修課同學好像有幾份作業他後半寫不完直接交,結果滿分25他還能拿23~24,所以陳俊全的分導應該和其他教授的比起來真的涼不少。
值得一提的是,我還蠻喜歡助教出的作業題目的,很大部分的題目都是他的自命題(都是心血啊)而不是直接從課本上抓。有一個小趣事是,有一次作業要我們構造出一個滿足兩個條件的ordered field,
- Cauchy Complete(所有Cauchy Sequence收斂在那個field裡面)
- 不滿足Archimedean Property
結果有很多同學都寫了同一個錯的答案,然後助教就把他出在下一次的作業裡,要我們證明他甚至連ordered field都不是,到底為什麼會交這種答案上去啊。
雖然課程要求有線代,不過我只有在norm space和inner product space那邊有卡住一下而已,大概一次上課的內容,那次作業有一題我還是去翻Friedberg第六章看了點提示才知道怎麼寫的。除此之外,我暑假有花時間看數學系微積分的錄影,這對我的幫助還蠻大的,因為我覺得我在微甲沒有很好的熟悉ε-δ語言,跟著錄影做過幾遍以後讓我比較能了解這個證明的思想了。
不過還是得說,花時間構造實數我覺得還是有點好處的,尤其是讓我深刻體會到實數到底是個多棒的東西,以及要造出這麼棒的東西原來是這麼麻煩的一件事,這也讓我後半學期寫作業時有時候卡住一秒,心想:「喔對實數的性質很棒」然後才寫下式子,以前聽過微積分的起點是實數的完備性,現在才總算了解了為什麼。
至於考試的部分,期中考是考三個小時的8選5,和以往課程評價裡寫的一樣,期末考好像是因為他教不完?這是我聽不到的部分內容之一所以被迫只能考在兩小時的那一天,因此改成6選4,題目應該不算難,固定會有兩題的上課大證明,然後剩下要補的題數在考卷上可以找到足夠的基本題來補,不過我慘痛的教訓是一定要背上課證明,原本期末考只要考84分就能A+的,但是我因為時間規劃大燒雞所以沒背完上課證明,結果考出來的兩題上課證明我都要當場想怎麼證…現在想著還是很可惜。
蠻有意思的事,這學期的課上真的遇到不少數學之美的東西,比如Cardinality、Cantor Set等等,還發現原來數學之美講兩個集合的Cardinality相等的時候根本不是用定義來做的,而是偷開了分導課上用選擇公理證的定理。
這學期修完讓我覺得我不太適合這個教授的風格,每堂課都要看他遲到二十分鐘,而且學到得也沒有原本預期中多(半學期學構造實數真的有夠虧,相比之下分析一只用好像兩節課),尤其借了朋友分析一的筆記以後發現,好像他們班的東西比較好玩誒,下學期留下來繼續修的誘因不是很大,所以我可能會明年換教授以後再來把分導二補掉吧!
小結與展望
可以來回顧一下前言提到的三個課表值得一提的點:
- 退SP修分導:我覺得現在還不太能說這個決定到底是好是壞,這很顯然同時有好處也有壞處,不過具體到底哪一邊佔比比較重,或許要等到我畢業,或是更以後我才有辦法回答,畢竟我做這個決定本來就不是為了這學期想過多爽之類
- 修兩個線代:我覺得這個決定是對的,畢竟如果不雙主修的話本來就是兩邊都修,早修晚修都要修,選擇這個學期修的話或許比明年還要回憶線代的細節好,
更何況我確實洗到GPA了,認真講的話,修本系線代應該也可以當作預習線代二了 - 先修自動機:完美,我想不到任何理由來支持不這學期修
不過我不認為我這學期有把成績顧好,我覺得很大部分的原因是我期末鬆懈了,雖然前面心得裡沒直接指出來,不過呂線代、ADA和自動機三門課都是三次期考,另外兩門數學系的課是兩次期考,因此除了期末考外,所有的期考都相當分散,學期前半段可以說過得相當輕鬆。但是到了期末考,呂線代和分導都在加緊救已經落後的進度,然後又五科同時考的狀況下,我確實沒複習好期考的內容,不然照著原本的感覺,線代和分導都不該只有A-的。
雖然系排被數學系送下去了,不過我還是覺得讀那些比起讀SP之類的更有趣,所以我下學期還是會繼續在課表裡填數學課,其實因為ADA的成績超級晚出來,所以現在下學期的初選一階已經截止了,我的志願序裡只有OS和機率是系上的課,不過如果機率導論選上了就只剩OS了。除此之外,因為我六學分的探索學分快要過期了,我也打算挑幾門電機系看起來有意思的課來探索一下。
但是與此同時我也在想,我這樣搞課表的話,學到的東西可能對未來工作都沒有幫助,簡單的說,我的職場生活是黑白的,也有可能我根本沒有職場生活,就不用管是黑白還是彩色的。我不知道我該維持興趣導向的選課路線多久,如果我畢業時找不到工作,又因為稀爛的GPA所以沒研究所念,我還真的不知道該怎麼辦。
學分統計
- 共同必修:6/9
- 系訂必修:29/51
- 輔系必修:9/23
- 選修
- 系訂選修:9/21
- 院內選修:0/9
- 一般選修:0/23
- 通識:7/15 $\colorbox{white}{A1}$ $\colorbox{LimeGreen}{A2}$ $\colorbox{white}{A3}$ $\colorbox{LimeGreen}{A5}$ $\colorbox{LimeGreen}{A8}$
- 體育:2/4
Overall:60/151